My track record

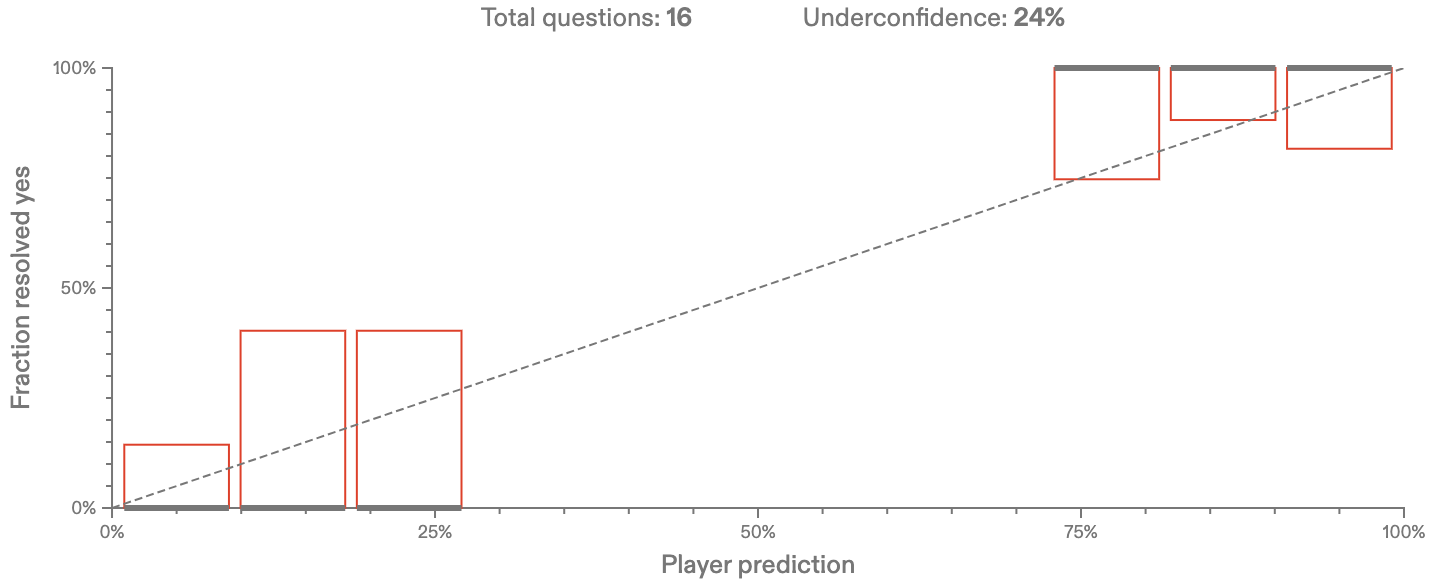
My binary calibration on Metaculus questions:

I am peter_m (click for a list of my comments) on Metaculus.

Up until now not enough questions (16 binary questions, 5 real-valued questions) have resolved to provide proof beyond doubt that I am well-calibrated or sharp (=not too over-/underconfident; for statisticians: By way of analogy to point estimators, calibration is like unbiasedness and sharpness is like precision (i.e., inverse variance).)

In fact, data weakly indicates that I am underconfident.

Finding “arbitrage opportunities”

Since Metaculus is not a market, but an information aggegrator, “arbitrage opportunity” does not appear to be a well-defined concept. Thinking of arbitrage as logical inconsistency (the kind of inconsistency that allows you to extract risk-free money from a market; or at least a positive amount of money in expectation), however, we might simply interpret this as a question of whether the community prediction is “consistent over time”.

The key idea is that the evolution of forecasts over time \((p_t)_{t}\) must be given by a martingale. This implies various bounds and equalities that are model and data agnostic! (I.e. we don’t have to make any assumptions whatsoever for these bounds&equalities to be necessarily true for sensible forecasts.)

In this notebook I find that the Metaculus community overreacts a little bit, whereas a weighted forecast (better predictors’ forecasts contribute more) performs better.
In this notebook I discuss the above ideas in more detail and work out what it implies for actual betting markets, e.g. how to come up with your own betting strategies to capitalise on different martingale violations.